Опционы — инструмент спекуляций и хеджирования
Рассмотрим простой, элементарный пример определения цены опциона с
учетом всех основных факторов влияния на его стоимость.
Возьмем, например, акции условной компании АВС. Предположим, что
мы уже обладаем пакетом этих акций в размере 1000 штук. При этом мы
знаем, что:
— текущая рыночная цена одной акции АВС равна $16;
— процентная ставка по безрисковому долговому инструменту составляет 5% годовых;
— периодичность выплаты процентов один раз в год;
— временной горизонт (рассматриваемый срок инвестиции) два года;
— компания выплачивает дивиденды в размере $0.6;
— периодичность выплаты дивидендов один раз в год.
Для начала всех этих знаний нам будет достаточно, поэтому попробуем рассмотреть различные варианты стоимости опционов.
Первым делом нам необходимо будет определить будущую, фьючерсную цену акций компании АВС, которая является справедливой и для держателя и для потенциального покупателя этих ценных бумаг.
Если мы сейчас продадим наш пакет акций АВС по текущей рыночной цене в $16 за штуку, то сможем получить $16000.
Дальше мы можем вложить эти деньги в безрисковый актив и получить процентный доход в сумме $1640.
Вместе с тем, продав акции, мы не получим дивиденды за два года на общую сумму $1230.
А если мы просто продали акции и вложили полученные деньги в безрисковый актив, то мы получили бы через два года $17640 (16000+1640).
Если же мы оставили бы эти акции в своем распоряжении, то через два года мы имели бы 1000 акций компании АВС и $1230. При вложении последней суммы в покупку дополнительного пакета акций АВС, при условии стабильности цен этих ценных бумаг, через два года мы имели бы почти 1077 акций (1000+1230/16).
Разделив $17640 на 1077, мы получим справедливую будущую стоимость акций компании АВС через два года — $16.38.
Похожую величину мы можем рассчитать также гораздо более простым путем, исходя из стоимости одной акции.
Справедливости ради надо заметить, что последний способ не только более простой, но и гораздо правильнее. Объясняется это допущением покупки акций компании АВС на дивиденды по цене $16 за штуку. На самом деле на момент инвестирования дивидендов акции компании АВС уже должны будут вырасти в цене до $16.41. То есть реально мы сможем купить не 77 акций, а 75.
Конечно же, нельзя говорить о том, что фьючерсные цены и реальные цены в будущем совпадают. Иначе просто достаточно было бы смотреть старые котировки (например, трехмесячной давности) фьючерсов на акцию, для того чтобы ожидать соответствующей рыночной цены этой ценной бумаги.
Вместе с тем, если реальная фьючерсная цена будет ниже справедливой, у держателя акций будет стимул продавать свои пакеты по текущим рыночным ценам, вкладывать полученные деньги в безрисковые активы для получения процентов на вложенный капитал и одновременно покупать фьючерсные контракты. Рост объемов спроса на последние должен будет поднять их стоимость до той величины, когда совершать подобные сделки будет уже невыгодно.
Похожую логику с точностью до наоборот можно будет применить для случаев, когда реальная фьючерсная цена оказывается выше справедливой.
После определения фьючерсной цены акции компании АВС через два года можно перейти к рассмотрению примеров со стоимостью опционов.
Например, нам предлагают продать колл-опцион со страйком $16.50 и сроком до экспирации два года, а также премию в $1.5 за контракт.
Здесь необходимо помнить, что текущая стоимость суммы премии на наш пакет акций 1000 штук будет составлять больше $1500 (1000Х1.5). Больше на величину процентов, т.е. на $153.75 (). Таким образом, реальная величина премии будет составлять $1653.75 (1500+153.75), или около $1.65 в расчете на одну акцию.
Точка безубыточности для покупателя этого колл-опциона составит $18.15 (16.50+1.65). То есть если рыночная цена акций компании АВС через два года составит $18.15, то покупатель колл-опциона исполнит его по цене исполнения (купит наш пакет акций в количестве 1000 штук) $16.50, полностью отбив величину ранее уплаченной премии, включая недополученные проценты. Мы при этом продадим акции фактически по цене $18.15 за штуку, что значительно выше ранее рассчитанной справедливой цены в $16.41. Если же рынок пойдет выше и рыночные цены поднимутся, например до $19, то продажа колл-опциона уже не будет самой эффективной стратегией — рынок будет идти без нас.

С другой стороны, нам также необходимо знать, падение цены акции ниже какой величины приведет продавца колл-опциона к убыткам при условии, что эти ценные бумаги будут по-прежнему оставаться в нашей собственности. Эта величина рассчитывается очень просто:
16.41 — 1.65 = 14.76.
То есть если стоимость акций АВС через два года упадет ниже $14.76 (за точку отсчета здесь в отличие от определения верхней границы безубыточности колл-опциона берется справедливая фьючерсная цена), то продажа колл-опционов и получение премии по ним не покроет убытки от падения котировок. Если реальная рыночная цена через два года окажется ниже $14.76, то более оптимальной стратегией было бы еще в самом начале продать акции и не ввязываться в продажу колл-опциона.
Итак, верхняя граница безубыточности для продавца колл-опциона составит $18.15. а нижняя — $14.76.
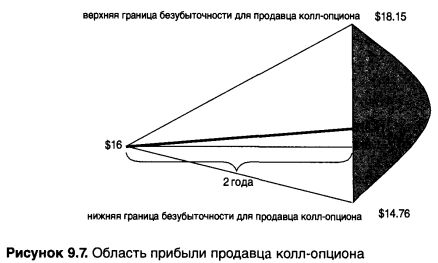
Для покупателя колл-опциона, если он все-таки реально заинтересован в приобретении означенного количества акций, нижняя точка безубыточности будет составлять $14.85 (16.50 -1.65).
Теперь остается совершить последний шаг — определить вероятность того, что рыночная цена через два года останется в границах безубыточности. Здесь-то и помогает знание волатильности (стандартного отклонения) рынка. И именно этот-то вопрос и является главным в определении стоимости опциона, главным и неизвестным. Недаром говорят: волатильность является объектом торговли в опционах.
Историческая волатильность может при этом навредить — достаточно вспомнить последствия изменения темпов падения рубля в августе 1998 года для российских банков. Плавное движение котировок рубля против доллара США в рамках валютного коридора практически в одночасье сменилось «штормом», разбившим не одну стратегию и расчет. Именно поэтому при работе с опционами рекомендуется использовать в первую очередь внутреннюю волатильность, историческую лишь имея в виду.
Как же рассчитать и откуда взять внутреннюю волатильность? Одним из самых простых способов является получение значения такой волатильности напрямую с рынка, уже оценивающего подобные опционы. Можете также попытаться скорректировать превалирующую на рынке внутреннюю волатильность на значение средней исторической волатильности выбранного инструмента. Результатом определения внутренней волатильности станет значение стандартного отклонения.
Итак, закончим наше маленькое исследование сермяжной правды опционов.
Для этого нам необходимо оценить вероятность того, что цена через два года (здесь также необходимо сделать предположение о колл-опционе как опционе европейского типа) останется в коридоре от $14.76 до 18.15, т.е. продажа колл-опциона будет являться экономически целесообразной.
Зная внутреннюю волатильность выбранного инструмента для заданного периода времени (два года), по формуле (3.13) можно рассчитать вероятность роста цены выше верхней границы ($18.15) и вероятность падения ниже нижней границы ($14.76).
Например, при значении стандартного отклонения акций компании АВС в 2.4 на периоде в два года вероятность составит
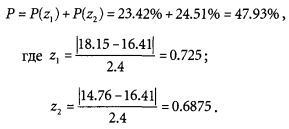
Таким образом, получается, что вероятность того, что рыночная цена через два года останется в расчетном коридоре от $14.76 до $18.15, составляет 52.07% (100% — 47.93%).
Дальше можно рассчитать, насколько целесообразна продажа колл-опциона, для чего используем формулу математического ожидания:
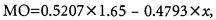
где х — средняя сумма убытка, который получит продавец колл-опциона с вероятностью 47.93%, оставивший в своей собственности пакет акций компании АВС.
Данная величина, к сожалению, неизвестна. Однако можно рассчитать цену, где математическое ожидание продажи колл-опциона окажется нулевым, нулевым отдельно для верхней и нижней границ:
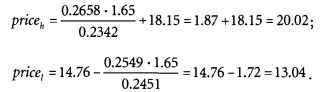
То есть если рыночная цена окажется в пределах от $13.04 до $20.02, то математическое ожидание получения прибыли от продажи колл-опциона для его продавца будет положительным. То есть если мы ждем, что рынок останется (теперь уже с вероятностью максимально близкой к 100) в пределах от $13.04 до $20.02, то продажа колл-опциона с оставлением акций компании АВС в своей собственности будет экономически целесообразной. Соответственно покупателя колл-опциона будет интересовать эта сделка, если он ожидает снижение цены или ниже $13.04 (если, конечно же, он действительно хочет купить акции), или выше $20.02.
Вот так вкратце выглядит элементарная логика определения стоимости опционов, во главе угла которой стоит оценка экономической целесообразности через математическое ожидание.
Основным узким местом при этом является знание внутренней волатильности базового актива, на который выписывается опцион (стандартного отклонения).
Если вы захотите рассчитать теоретическую стоимость опциона с использованием более серьезного и точного подхода, то для это можно использовать одну из следующих моделей.
Есть несколько различных теоретических моделей зависимости цены опциона от перечисленных выше переменных. Эти модели различаются особенностями оцениваемых активов (акций, товаров, фондовых индексов, валют и т.п.), а также отличаются от сделанных предположений. В то же время все эти модели используют формулы для расчета «справедливой» цены (fair price) при текущих значениях переменных и по этой причине цены, полученные при расчете каждой модели, сильно не различаются.
Теоретические модели помогают оценить, сколько должен стоить конкретный опцион в конкретный момент времени, хотя полученная оценка и не будет являться истиной в последней инстанции.
Однако, как правило, встречается ситуация, когда реальная цена сильно отличается от цены «справедливой». В подобных ситуациях в теоретической модели вместо исторической волатильности, которую вычисляют по предыдущим данным ценового ряда, используется другая ее величина. Последняя подбирается так, чтобы справедливая цена совпала с реальной рыночной. Как мы уже знаем, эту волатильность называют внутренней (implied volatility). Этот подход хотя и ущербен в силу отсутствия строгой научности, но широко применяется практиками торговли опционами.
Использование теоретических моделей ценообразования опционов позволяет трейдерам вычислять прогнозную стоимость опциона в будущем. Если трейдер имеет какие-либо предположения о дальнейшем развитии рынка (например, через 15 дней цена актива вырастет на 5%, волатильность уменьшится на 2%, а процентная ставка останется неизменной), то он может рассчитать будущую цену опциона.
Наиболее распространенной моделью для расчета цены опциона является модель Блэка — Шоулса (Black — Scholes), разработанная Фишером Блэком (Fischer Black) и Майроном Шоулсом (Myron Scholes) в начале 70-х годов. Кстати, за развитие теории ценообразования опционов Роберту Мертону (Robert Merton) и Майрону Шоулсу в 1997 году была присуждена Нобелевская премия по экономике. Эта модель хорошо описывает ценообразование европейских опционов на акции. Узким местом модели Блэка Шоулса является неизменность волатильности в течение жизни опционов со всеми ценами исполнения, а также подчинение цен случайному процессу с логнормальным распределением. Согласно модели Блэка — Шоулса премия опциона колл европейского стиля находится в прямой зависимости от цены базисного актива, волатильности, количества дней до экспирации и безрисковой процентной ставки, а также в обратной зависимости от цены исполнения.
Формулы для расчета стоимости европейских опционов колл и пут в модели Блэка — Шоулса выглядят так:


Один из наиболее распространенных вариантов расчета волатильности (логарифмический) выглядит следующим образом. Сначала рассчитывается ряд логарифмов изменения цен:
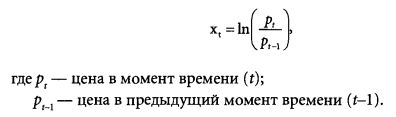
Далее рассчитывается среднеарифметическое ряда значений х, за некоторый ограниченный период времени:
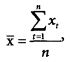
где и — некоторый ограниченный период времени, за который рассчитывается волатильность (например, 10,20, 30, 60, 90, 120, 150 или 180 дней).
Далее рассчитывается историческая волатильность за этот ограниченный промежуток времени
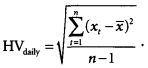
Затем приведем рассчитанную выше историческую волатильность за
некоторый промежуток времени к годовому значению
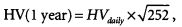
где 252 — количество рабочих дней в календарном году.
В формуле Блэка — Шоулса размер премии зависит от шести параметров:
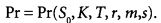
Значения всех параметров, кроме т, мы уже рассмотрели раньше. Параметр задается в зависимости от вида базисного актива:
т = r — для опционов на акции, по которым не выплачиваются дивиденды;
m = r — q — для опционов на акции, по которым выплачиваются дивиденды с заданной непрерывной ставкой q;
m = r — rf — для валютного опциона, где r — безрисковая ставка процента в валюте торговли, а rf — в базисной валюте;
m = r — q — для опционов на фондовые индексы, где q — средняя ставка дивидендов, которые выплачиваются по включенным в индекс акциям в течение срока опционного контракта;
m = 0 — для опционов на фьючерсные контракты, причем здесь St — текущая фьючерсная цена;
m = r — q — для облигационных опционов, где q — приведенная купонная процентная ставка, а St — текущая цена базисной облигации.
|