В своей книге “Мастер-трейдинг: секретные материалы” Эрик Найман в доступной форме представил все основные элементы успешного трейдинга: определение фундаментальной основы возникновения тренда, работа на рынке по осцилляторам, уровни как точки опоры для прибыльного трейдинга, теории изменения рыночных цен и т.п.

Многое из ранее сказанного дает нам основание относиться к рыночным явлениям как к случайным и соответственно применять теорию вероятностей (theory of probabilities). Таким образом, без понимания теории вероятностей предпринимать последующие шаги вряд ли имеет смысл.

Вероятность представляет собой количественную меру того, что какое-либо случайное событие произойдет. Вероятность может принимать значение в промежутке от 0 (невозможное событие) до 1 (событие, которое обязательно наступит). Иногда вероятность описывают в процентах. В этом случае нижняя и верхняя границы значения вероятностей будут равны 0 и 100% соответственно. Классическая формула для определения вероятности наступления случайного события х выглядит следующим образом:

Слава Україні!

Адмін сайту, який є громадянином України та безвиїзно перебуває в Україні на протязі всього часу повномасштабної російської агресії, зичить щастя та мирного неба всім українським хлопцям та дівчатам! Також він рекомендує українським трейдерам кращих біржових та бінарних брокерів, що мають приємні торгові умови та не співпрацюють з російською федерацією. А саме:

Exness – для доступу до валютного ринку;

RoboForex – для роботи з CFD-контрактами на акції;

Deriv – для опціонної торгівлі.

Ну, і звичайно ж, заборонену в росії компанію Альпарі, через яку Ви маєте можливість долучитися як до валютного ринку, так і до торгівлі акціями та бінарними опціонами (Fix-Contracts). Крім того, Альпарі ще цікава своїми інвестиційними можливостями. Дивіться, наприклад:

рейтинг ПАММ-рахунків;

рейтинг ПАММ-портфелів.

Все буде Україна!

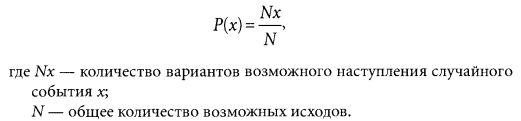
Пример. Бросая игральную кость, мы можем получить шесть возможных исходов — выпадение одной из шести граней игральной кости: 1, 2, 3, 4, 5 или 6. Таким образом, можно определить вероятность выпадения одной из граней, например 3:

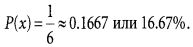
Таким образом, вероятность выпадения одной из граней игральной кости (в нашем примере 3) составляет 16.67%.

Можно также определить вероятность выпадения одной из двух граней (например, 2 или 3). В этом случае используется правило сложения вероятностей, а вероятность рассчитывается следующим образом:

Таким образом, вероятность выпадения грани с цифрой 2 или 3 равна 33.33%.

Правило сложения вероятностей используется для зависимых событий, когда одно случайное событие исключает наступление другого случайного события.

Если необходимо найти вероятность одновременного наступления двух и более случайных событий, используется правило умножения вероятностей. При этом все события должны быть независимы друг от друга.

Пример. В результате одновременного броска двух игральных костей мы можем получить 36 различных комбинаций: 1 — 1, 1 — 2, 1 — 3, 1 — 4, 1-5, 1 — 6, 2 — 1, 2 — 2, 2 — 3 и т.д. Для определения вероятности того, что в результате подбрасывания мы получим на гранях обеих игральных костей по 1, используем правило умножения вероятностей:

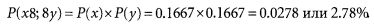
Таким образом, вероятность одновременного выпадения на двух игральных костях граней с цифрой 1 равна 2.78%.