Практический пример расчета теоретической цены опциона
В качестве примера рассчитаем теоретическую стоимость опциона колл
на фьючерсный контракт на курс фондового индекса S&P 500.
Начальные условия.
Тип контракта — американский.
Дата исполнения — 21 мая 1999 года.
Текущая дата — 15 апреля 1999 года.
Т — доля года, оставшаяся до истечения опциона (отношение количества дней до истечения опциона к 365). На текущую дату срок до истечения опциона составляет 36 дней. Таким образом, оставшаяся до истечения опционного контракта доля года равна 0.09863.
е — экспонента. Численная константа 2.71828182845905.
К — страйк равен 1325.
S, — цена фьючерсного контракта на курс фондового индекса S&P 500 в момент покупки опциона равна 1323.
r — безрисковая процентная ставка равна 10%.
s — внутренняя волатильность равна 17.43.
m = r — q. Если q — сумма планируемых к выплате дивидендов держателю акций с момента эмиссии опциона равна 0, то m = r, т.е. m = 10%.
Отсюда рассчитаем
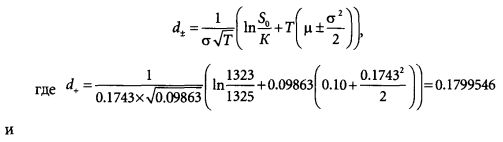

Таким образом, теоретическая стоимость опциона на фьючерсный контракт на курс фондового индекса S&P 500 с указанной выше спецификацией составляла 34.58.
Реальная стоимость этого опциона на рынке составляла 34.60, что практически точно совпало с полученной нами оценкой.
Премии опционов можно рассчитывать при помощи так называемых опционных калькуляторов. Так, калькулятор для американского рынка акций находится на web-странице чикагской опционной биржи СВОЕ:
http://www.cboe.com/TradTool/OptionCalculator.asp.

Модель Блэка — Шоулса исходит из целого ряда допущений, некоторые из которых являются критическими. Так, в модели не учитываются дивиденды, которые платит акционерная компания в течение срока действия опциона. Это допущение легко избежать, если вычесть ожидаемую величину дивидендов из премии, предварительно продисконтировав ее (скорректировав на безрисковую процентную ставку). Другим допущением модели Блэка — Шоулса является то, что она рассчитана только на опционы европейского типа. Третье предположение — что рынки являются эффективными, а динамика рыночных цен случайна. Это, пожалуй, самое спорное допущение, отражаемое в использовании трейдерами внутренней, а не исторической волатильности. Также следует отметить, что в модели Блэка — Шоулса совершенно не учитывается уровень комиссионных и других обязательных платежей, которые осуществляет трейдер опционами.
Модификацией модели Блэка — Шоулса для опционов на фьючерсы является модель Блэха (Black). Фишер Блэк разработал эту модель в 1976 году специально для оценки опционов на фьючерсы. При этом он рассматривает фьючерс как акцию, которая не приносит дохода свыше безрисковой процентной ставки.
Модель Кокса — Росса — Рубинштейна (Сох — Ross — Rubinstein) учитывает факторы, которые не рассматриваются в модели Блэка — Шоулса и являются усовершенствованным вариантом биномиальной модели. Вместе с тем, модель Кокса — Росса — Рубинштейна дает результаты, близкие к модели Блэка — Шоулса. Отличие этих двух моделей заключается в учете возможности досрочного исполнения американского опциона, что очень важно при высокой безрисковой процентной ставке.
Модель Гармана — Кольхагена (Garman Kohlhagen) создана специально для оценки опционов на валюты. В этой модели валюта рассматривается как актив, который приносит доход на уровне безрисковой процентной ставки.
Модель Мертона (Merton), модель The Barone-Adesi-Whaley Quadratic model, разработана в 1973 году. Эта модель исходит из случайного характера изменений безрисковой процентной ставки, что является лучшим отражением действительности, нежели допущения предыдущих моделей. Обычно модель Мертона используется для европейских опционов на акции. Также она дает неплохую оценку стоимости опционов на фьючерсы и более точные оценки для опционов «вне денег».
Модель Дмитрия Буртова учитывает основной недостаток, присущий перечисленным выше моделям — предположение о неизменности волатильности для опционов с различными ценами исполнения. Для расчета теоретической цены опциона в модели Буртова используется кривая доходности (Yield Curve), построенная на основании вчерашних цен закрытия (Yesterday Settlment). Расчет цены опциона включает в себя следующие шаги:
а) оценку вчерашней кривой доходности и сегодняшней доходности конкретного опциона. Оценка проводится по модели Блэка;
б) определение сдвига вчерашней кривой доходности относительно сегодняшнего ее значения;
в) расчет средневзвешенной кривой доходности на базе вчерашней и сегодняшней кривой с учетом тиковых объемов (Tick Volume) в качестве весов для различных страйков (вчерашний тиковый объем полагается равным 1). Например, если сегодняшний тиковый объем для рассматриваемого опциона равен 4, то результирующая кривая доходности в точке, соответствующей данному страйку, будет находиться на дистанции 4/5 между вчерашней и сегодняшней кривой доходности, располагаясь ближе к сегодняшней;
г) полученная доходность подставляется в формулу Блэка для расчета цены и коэффициентов греческой таблицы опциона.
При использовании всех перечисленных выше моделей предполагается, что цены изменяются по логнормальному распределению. Однако в реальных условиях это условие не всегда выполняется. Согласно теории хаоса рынок не является случайным, а значит, и нормально распределенным. Это замечание относится как к развитым, так и к развивающимся рынкам. Эффект отклонения изменения цен от нормального распределения наиболее заметен для опционов с малой стоимостью. Это объясняется тем, что участники рынка всегда помнят о возможном экстремальном движении цен базового актива, которое приведет к сильному увеличению стоимости данных опционов, а значит, их реальная рыночная стоимость обычно оказывается более высокой, чем это следует из формулы БлэкаШоулса. Данный эффект носит название «улыбка волатильности» (volatility smile).
Модель Монте-Карло эксплуатирует классический метод Монте-Карло, который оценивает среднее значение некоторой случайной величины. Применительно к расчету премии опционов модель Монте-Карло сводится к оценке математического ожидания премии (здесь дана оценка премии европейского опциона колл):

Для расчета премии американских опционов необходимо построить на интервале моделирования от 0 до Т равномерную сетку и оценить дисконтированный средний выигрыш во всех узлах, ключевых точках сетки по формуле

В заключение отмечу, что торговать опционами также лучше всего
от сильных уровней сопротивления и поддержки.
Так, покупать коллы хорошо от сильного уровня поддержки.
Покупать путы — от сильного уровня сопротивления.
Продавать коллы — от сильного уровня сопротивления.
Продавать путы — от сильного уровня поддержки.
Покупать стрэддлы (одновременная покупка колла и пута с одной
ценой исполнения) — от сильных уровней сопротивления или поддержки.
Продавать стрэддлы — на уровнях жизни.
|